Параметры и элементы электрической цепи

Параметрами электрической цепи называется величина, связывающая ток и напряжение на конкретном участке цепи (r – сопротивлением, L – индуктивностью, C  – ёмкостью).

Элементами электрической цепи называют отдельные устройства входящие в электрическую цепь и выполняющие в ней определённую функцию. Пример отдельных элементов и простой схемы электрической цепи:

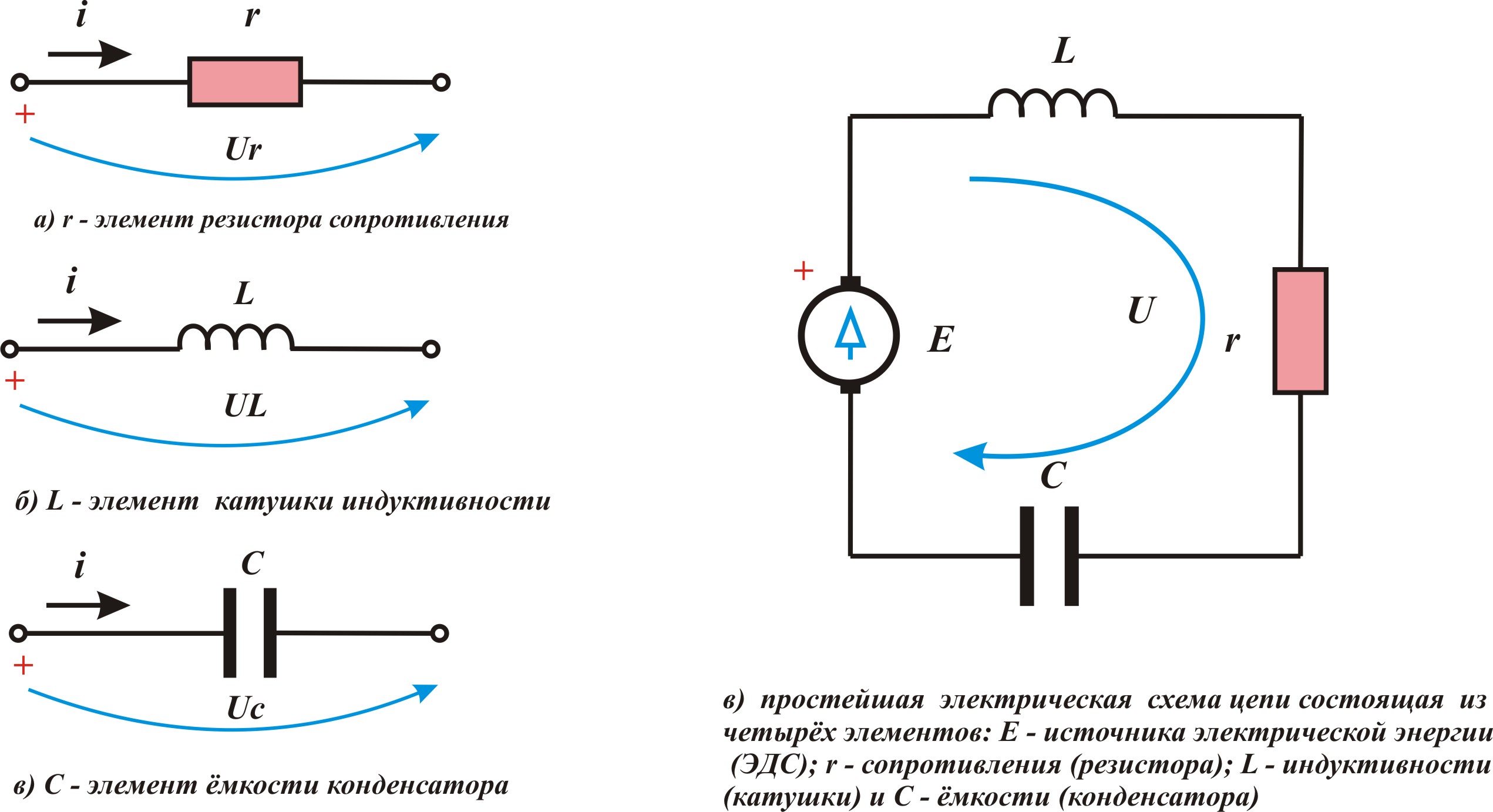
Рис.2

Схемы электрических цепей

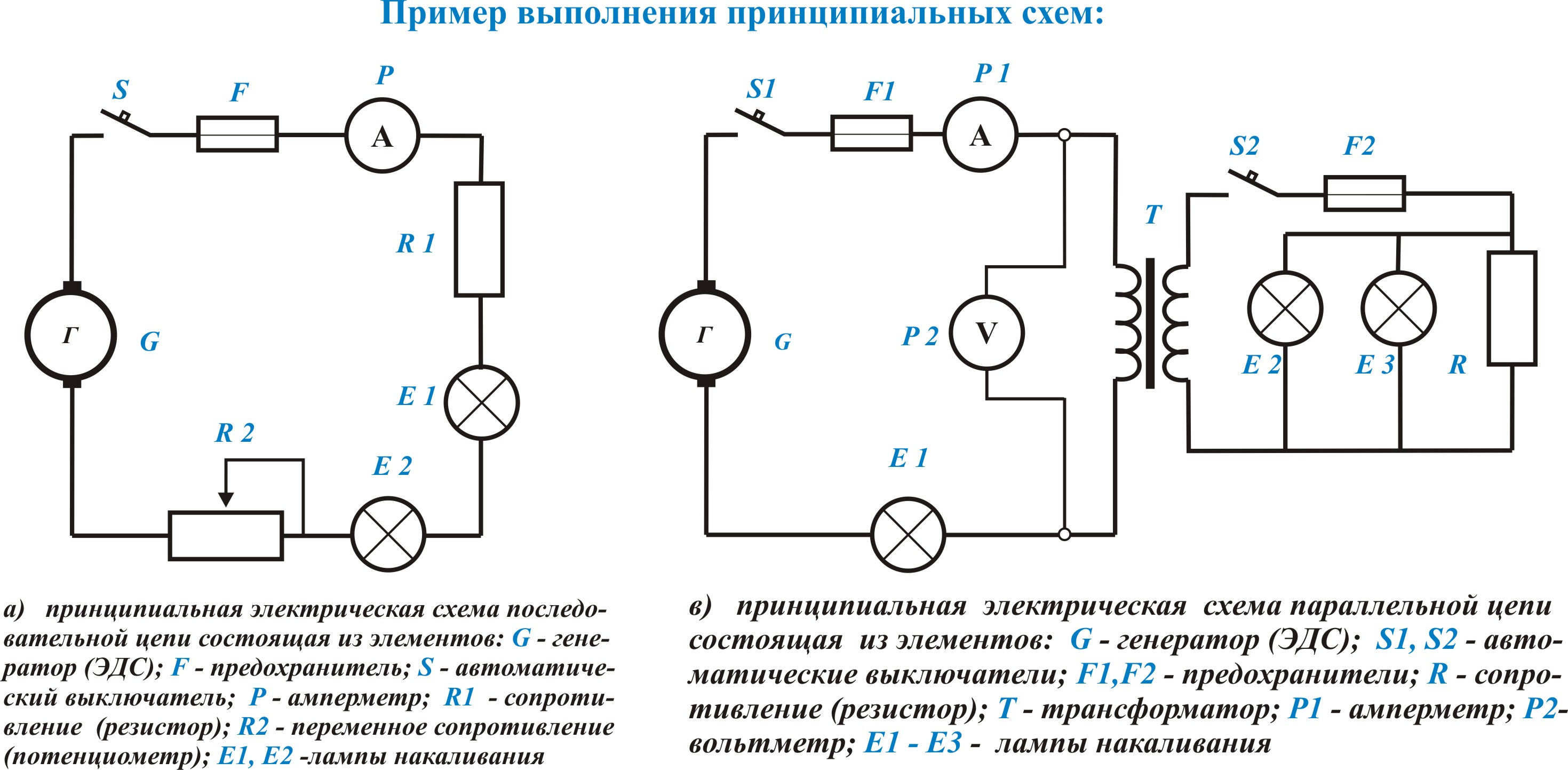
        При конструировании, монтаже и работе электрических установок (электрооборудования) нельзя обойтись без электрических схем. Электрические схемы по своему назначению различаются на несколько типов: структурные, функциональные, принципиальные, монтажные, однолинейные, и др.

        Принципиальная схема даёт полное представление о работе электроустановки, полный состав элементов и связи между ними.

         Схема электрической цепи – это графическое представление изображения электрической цепи, которая содержит условные обозначения элементов и соединение этих элементов. Условные обозначение в электрических схемах установлены стандартами системы ЕСКД. Различают последовательное и параллельное соединение элементов в схемах и электрических цепях. Сложные электрические схемы образуются в результате включения групп элементов соединенных между собой последовательно или параллельно (см. на рис.).

Электродвижущая сила (ЭДС)

       Физические процессы получения электрической энергии различаются в зависимости от вида преобразуемой энергии, где главное различие состоит в природе сил, которые разделяют положительный и отрицательный заряды в веществе. На электрически заряженные частицы кроме сил электрического поля при определенных условиях действуют сторонние силы, обусловленные неэлектромагнитными процессами (тепловые процессы, химические реакции и т.д.)

       В результате действия сторонних сил в источнике электрической энергии происходит разделение электрических зарядов и образуется электродвижущая сила (ЭДС).

      Величина, характеризующая способность стороннего поля и индуцированного электрического поля вызывает электрический ток, называется электродвижущей силой.

     Для примера рассмотрим преобразование тепловой энергии в электрическую:

В замкнутой цепи из двух разных металлов при одинаковой температуре (контактов 1 и 2) электрический ток не возникает, так как контактные разности потенциалов в обоих контактах  одинаковы, но направлены в противоположные стороны по цепи:

     Рис.4

Схемы замещения электрических цепей. Топологическое свойство цепей.

    Для облегчения расчета составляется схема замещения электрической цепи, на схеме замещения изображаются все элементы цепи, влияниями которыми нельзя пренебречь, а также указывают электрическое соединение между ними.

   Прежде чем перейти к структуре составления схем замещения напомним термины и определения:

• Топология -  это раздел математики, изучающий неколичественное соотношения между геометрическими объектами.
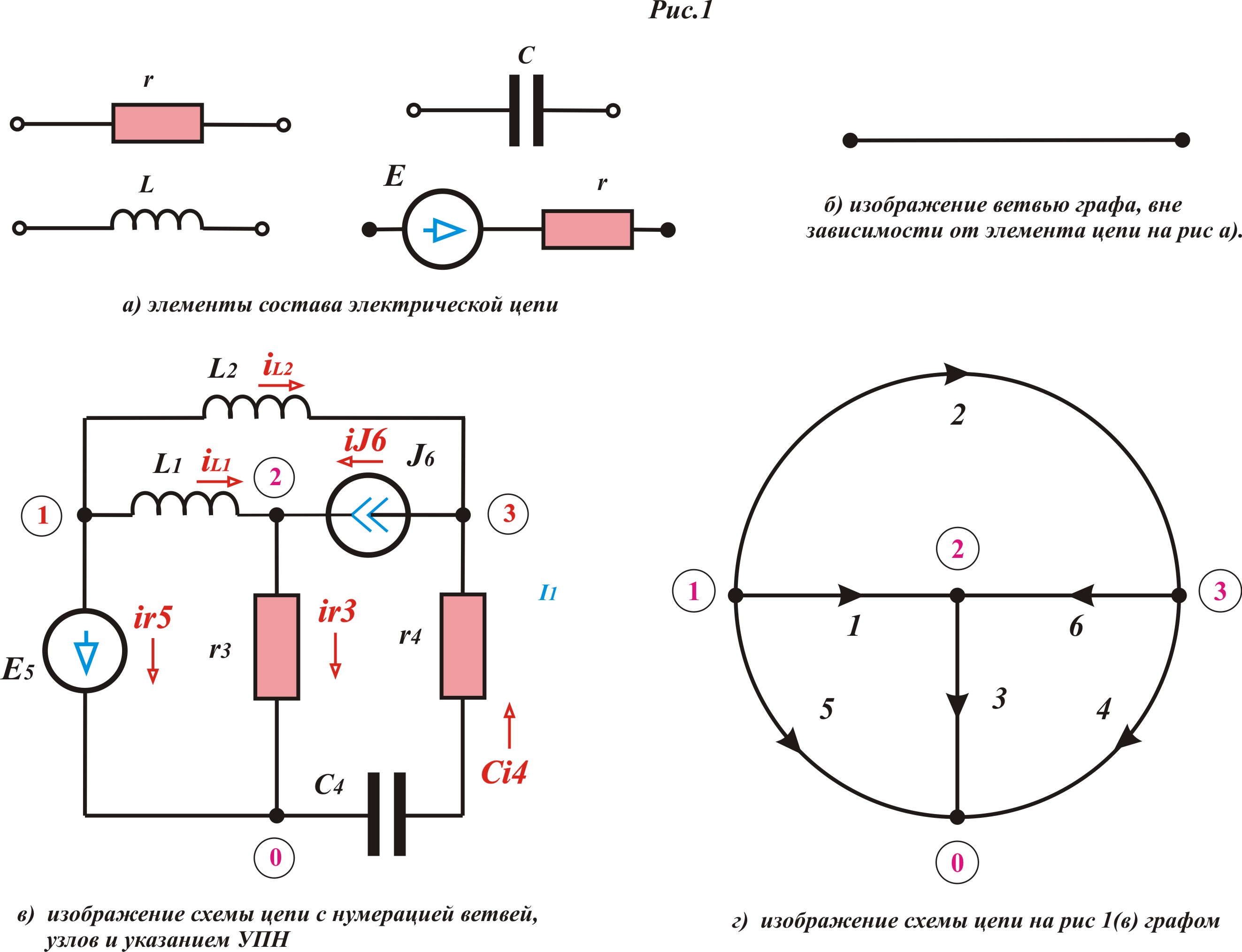
• Схема – основное топологическое понятие теории цепей, это графическое изображение модели цепи, состоящая из ветвей и узлов.
• Ветвь – участок цепи с неизменным током.
• Узел – место соединение трёх и более ветвей (формально узлом можно считать место соединения двух ветвей, такой узел называют простым, например разделяющая точка соединения двух последовательных ветвей, для обозначения на схеме).
• Граф –  изображения цепи (ветви цепи) без информации об элементах цепи. Если в графе указан УПН (условно – графическое направления тока или напряжения), то такой граф называется направленным. Если цепи не связаны электрически (например: связаны только через магнитное поле) граф называется не связанным.

Основное топологическое понятия графа это - путь графа (последовательность ветвей, в которой ни один узел не повторяется). Ветви изображенные на рисунке ниже, вне зависимости от элементов, заменяются простой ветвью графа:

Замечание: при анализе простых электрических цепей с простой и наглядной схемой пользуются схемами замещения электрических цепей, к топологическим свойствам цепи прибегают при анализе сложных цепей с использованием вычислительной техники. 

Законы Кирхгофа

Основная цель расчета электрической цепи заключается в определении токов в её ветвях. Зная токи, нетрудно найти напряжения и мощность ветвей и отдельных элементов цепи. Связь между ЭДС, напряжениями и токами линейных электрических цепей выражается линейными уравнениями. Значения токов, напряжений и мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования во всех участках электрической цепи.

Для расчета электрических цепей с законом Ома применяются два закона Кирхгофа.

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам электрических цепей:

В ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

∑ I = 0. 

В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основание первого закона Кирхгофа для каждого узла можно составить уравнения токов. Например, для точки 2 (Рис. 5(в) и (г) ) уравнение имеет вид:

I1 + I6 – I3 = 0	В этом уравнении токи, направлены к узлу, условно взяты – положительные, а токи, направленные от узла – отрицательные.
I1 + I6 = I3.	В этом уравнение первый закон Кирхгофа можно сформулировать как: сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от того же узла.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрических цепей:

В контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

∑ U = 0.

Рис.6

Для доказательства второго закона Кирхгофа обойдём контур  по часовой стрелке (Рис. 6) 1-2-3-4-5-6-1 и запишем потенциалы точек контура по указанным направлениям токов в ветвях, которые выбраны произвольно. Обход начнём с точки 1, потенциал которой V₁. Потенциал следующей точки выразим относительно предыдущей: V₂ = V₁ + E₁; V₃ = V₂ – I₁; V₄ = V₃ - I₄; V₅ = V₄ – E₃; V₆ = V₅ + I₆; V₁ = V₆ – I₃.

Изменение потенциала по выбранному контуру должно быть равно нулю, т.к. оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приёмников энергии (см. Рис. 1). Тогда в замкнутом контуре: 

V₁ + V₂ + V₃ + V₄ + V₅ + V₆ = 0,    E₁ – I₁ – I₄ – E₃ + I₆ – I₃ = 0,

или   - (E₁ – I₁) + I₄ + (E₃ – I₆) + I₂ = 0.

Соответственно в этом уравнении напряжение ветвей:

               3 – 2 – 1         E₁ – I₁ = U_3,1;               4 – 5 – 6           E₃ – I₆ = U_4,6;                               

                     3 – 4          I₄ = U_3,4;                           6 – 1            I₂ = U_6,1,

поэтому U_3,1 + U_4,6 + U_6,1 = 0. В данном уравнении напряжения считаются положительными (по обходу контура), а направления против обхода – отрицательными.

Перепишем уравнение в следующем виде:

I₁ + I₄ + I₃ – I₆ = E₁ – E₃. 

В таком виде уравнение даёт другую формулировку второго закона Кирхгофа:

  В контуре электрической цепи алгебраическая сумма падений напряжения в пассивных элементах равна алгебраической сумме ЭДС этого контура:

∑ IR = ∑ E. 

Соответственно к другим контурам составляются другие уравнению, которые нетрудно составить, не прибегая к выражениям потенциалов точек контура, пользуясь простым правилом. В левую часть уравнения записывать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую алгебраическую сумму ЭДС, встречающихся при обходе контура. Соответственно положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода.